In art, it takes the form of mosaics, and in building and construction it appears as various forms of tiling for pathways and in decorative flooring.
The Islamic nations were the world leaders in tessellation for many centuries. Whereas much western art of the time concentrated on depiction of the human form, Islamic art was more of a geometric nature, with advanced tessellation a significant feature.
The Girh tiles are a set of five shapes used in producing striking tessellation patterns in Islamic architecture from about the year 1200 onwards. The patterns produced are highly complex, and are underpinned by some advanced mathematical concepts that were well ahead of their time. For some more details on the Girh tiles go to
http://en.wikipedia.org/wiki/Girih_tiles

The Alhambra Palace, Granada, Spain
Image: Wikipedia Commons (Click to enlarge)
Wonderful examples of tessellation can be found at the Alhambra palace in Granada, Spain, that was built in the early 1300’s. Although over 650 years old, highly advanced tessellations are present that would have been very difficult to construct at the time, without the benefits of computer technology.
Today, the computer makes tessellation accessible to everyone, with the Power Point software ideal for experimentation and manipulation of all types of shapes, either straight sided or curved.
There are many different approaches to tessellation, but here we will look a simple “freestyle” method which begins by constructing closed straight line figures of any shape, and then producing tessellations from these.

(Click on images to enlarge)

(Click on images to enlarge)

(Click on images to enlarge)

In this case all the four shapes have equal area - the original shape plus the space between. (Click on image to enlarge)

We now find that we have created a shape - outlined in red here, that is self tessellating and is composed of four shapes of equal area that are also self-tessellating. (Click on image to enlarge)
The obvious question is can we say this in reverse - that is can we subdivide any self tessellating shape into four equal areas that are also self tessellating?
The answer to this lies well beyond my abilities but I'm sure there are those out there in cyber-space that will know. I'd love to hear from you!
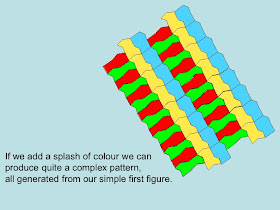
 Power Point also allows you to fill the shapes with images, producing interesting artistic effects. (Click to enlarge)
Power Point also allows you to fill the shapes with images, producing interesting artistic effects. (Click to enlarge)The master tessellator of modern times was undoubtedly M.C.Escher, a Dutch artist who combined the geometry of tessellation with conventional pictorial art. He was said to have been inspired by the tessellations he saw at Alhambra. The results are highly intriguing and produce a distinctive and unique art style.

Some of the exquisite tessellation
of the Alhambra
Image: Wikipedia Commons
An Intricate Escher tessellation
Image: Wikipedia Commons

Since I posed the question above "can we subdivide any self tessellating shape into four equal areas that are also self tessellating?" there has been one response - from Jo Edkins of the UK.
ReplyDeleteThis indicates that the answer is yes if we consider a figure that has opposite sides (curved or straight sided) that are the same. This is if course a special case and the jury is still out on the general case.
For further info about Jo see
http://gwydir.demon.co.uk/jo/tess/index.htm